Площадь двух треугольников
Какая у вас оценка в школе по геометрии? Впрочем, не важно…
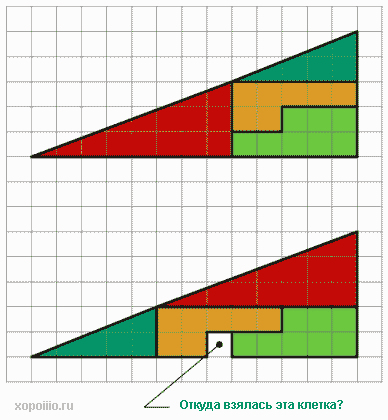
На картинке ниже вы видите 2 треугольника. Треугольники составлены из четырёх фигур. Площадь фигур, из которых состоят треугольники, одинакова. Что у верхнего, что у нижнего, можете вырезать из бумаги и проверить.
А теперь давайте перемешаем фигуры, что получится?
Как такое может быть? Откуда взялась эта пустая клетка? Невозможное возможно?! 🙂






 СМЕКАЛОЧКА - в примерах
СМЕКАЛОЧКА - в примерах  Интресные ФАКТЫ
Интресные ФАКТЫ
А мне кажется, что здесь все очевидно… 2 треугл. не больше потому что тот прямоугольник синий меньше чем красный. Все очевидно, хотя у меня по геометрии плохо.
Аналогично, почитал коменты… ё-маё, сколько ж у нас бестолочей!!! Выпуклые, впуклые, линии кривые, масштабы мелкие…. олени. Всё там ПРЯМОЕ, руки у вас кривые. Да вы хоть на все футбольное поле нарисуйте, будет тот же эффект! И причем нахрен не нужно рисовать 2 треугольника! При перестановке фигур в ОДНОМ!!! треугольнике появляется пустая клетка! Разуйте глаза!! И купите себе мозг!!!
Не стал дочитывать комментарии. Но меня бесят умники, которые говорят, что углы разные. Третий класс математики говорит (так как про подобие треугольников этим грамотеям нет смысла), что если прямая пересекается двумя параллельными прямыми, то образующиеся углы равны. Да здравствуют практики. Все съедает погрешность. Смысл в чем. Здесь изначально все проводится по клеточкам. и они здесь не относительно жирные, не только из-за того, чтобы мы могли по ним вырезать фигуры, а чтобы скрыть эту самую дельту. Нарисуйте в любой чертежной программе первый рисунок под формат А4. Рисуем треугольник, где должен поместиться пазл, потом рисуем вертикальную через 8 клеток от острого угла (чем тоньше линия, тем точнее получатся фигурки). И о чудо… Мы видим, что эта линия пересекает гипотенузу не точно по горизонтальной линии, а немного выше (где-то 10-я часть клетки). Теперь проводим остальные фигуры отталкиваясь от этой точки пересечения, распечатываем, вырезаем. Сначала у нас все совпадает, а когда переставляем фигурки в том порядке, что на втором рисунке, то у нас опять… О чудо получается квадратик. Однако вместе с тем уже видно, что эти фигурки не совсем сходятся, то есть где-то выходят за рамки треугольника, где-то накладываются друг на друга. Сразу отвечаю на вопросы пессимистов, в маленьком масштабе точность вырезания мала. плюс мозг подгоняет ответ задачи под увиденный ответ, поэтому не ленитесь, а начертите все с помощью чертежных программ на большом формате. И уже после первой вертикальной линии от острого угла вам все станет ясно. По-моему тема себя исчерпала))))))
ребята я блондинка, по геометрии у меня было 3, зато я умею прикладывать линейку к монитору, на первом треугольнике гипотинуза ( которую образуют 2 треугольника) -вогнута в нутрь, на втором – выгнута. за счет этой “дуги” освобождается пространство!!! здесь не надо геометрию.. тут чисто логически без расчетов все понятно!!
Люди, умницы, красавицы. Отбросьте на фиг треугольники красный и синий. Только две фигуры – желтая и зеленая. Три клетки узкой части желтой фигуры и две клетки узкой части зеленой фигуры. Они НИКОГДА НЕ СОВПАДУТ. В верхнем треугольнике желтая фигура лежит на зеленой. А в нижней они рядом (в тетрис сыграйте, умники)ТО ЕСТЬ ПУСТАЯ КЛЕТКА БУДЕТ ПО ЛЮБОМУ. А треугольники можете хоть по диагонали приляпать. Задание состоит в том, что бы понять откуда пустая клетка. Ответ, перестановка фигур – красный треугольник меняется местом с синим, а желтая и зеленые фигуры становятся рядом (это сделано для того, чтобы они ровно поместились под красный треугольник). Все. Не нужно делать из простого сложное. Вот если бы Вам задали задачу о площади этих фигур, тогда да. На четко поставленный вопрос должен быть четко поставленный ответ. А потом удивляемся, что у нас спутники падают, от таких-то спецов.
Что за чушь вы из себя выдавили? Спутники не падают, они на орбите, а падают ракеты, ступени и разгонные блоки. У рас пильщика бюджета США Илона Маска действительно падают, но многоразовой РАКЕТЫ он так и не показал, вместо этого скатился на многоразовые ступени, но и их он так и не создал, ведь он ни разу не отправил хотя бы два раза подряд один и тот же комплект ступеней. Лишь одну ступень из всего комплекта смог заново запустить и то только после того как 90% капитального ремонта в ней было произведено, а материальные и временные затраты составили больше 100% по сравнению с обычной новой ступенью)) И да у Илона Маска до сих пор не получилось создать ничего более надёжного, чем ракета Союз, не говоря уже про систему безопасности, которой нет аналогов в мире и сами американские астронавты это признают
Всё легко, достаточно провести прямую линию по гипотинузе, на верхнем русунке линия проваливается на нижнем наоборот выперает по центру. Если даже клеток 8 отсчитать от левого угла и посмотреть линию от низа то верха, то она имеет разную длинну. Вот за стёт того что гипотинуза играет (вверх вниз) и не является прямой линией, вот отсюда и берётся этот квадрат. )
vk.com/sivaliv
Ребята я думала,что те кто говорил о вогнутых и выпуклых гипотенузах посходили с ума,но попробуйте приложить линейку к гипотенузе, и вы увидите,что на нижнем рисунке она чуть выпуклая на месте соединения треугольников,а на верхнем чуть вогнута,так это совершенно не заметно пока точно не измерить.А из бумаги я тоже вырезала и лишняя клетка появляется,но форма самого треугольника меняется так как нижняя зеленая фигура чуть выпирает в бок,как раз давая жизнь лишней клетке.Я не понимала как на сайте у них все так обстряпано,теперь понимаю,что из за разности площадей,у нижнего чуть больше.
это не треугольники =/
Хорошая задача, познавательная. Скорее повторюсь, но попытаюсь донести для тех, кто не понимает. Эти две фигуры, верхняя и нижняя, не совсем треугольники. У верхнего гипотенуза чуть надломлена внутрь, у верхнего горб наружу.
Ради примера, начертите на тетрадном листе (это очень важно для понимания) Один треугольник с катетами 2 и 2 клетки, второй с катетами 2 и 4 клетки и если их сложите подобным образом, то разница будет не в 1 клетку, а в 6 клеток. Но даже на рисунке видно, что верхний треугольник вогнут чуть внутрь, а верхний наружу, но здесь это не так явно, из-за того, что разница между (тангенсами или котангенсами) катетами маленького и среднего треугольника не такая явная. Лишняя клетка появляется у того треугольника (он конечно не совсем треугольник, как и другой) где “горбинка” наружу.
Короче, я вчера до ночи всё здесь читала, читала. Дошла и до тангенсов, и до понятия “подобия” треугольников, и резала даже ножницами. Так вот, получается, что клетка эта лишняя размазана почучуть по всем фигурам верхнего треугольника. Конкретно эти треугольники действительно немного разные (выпуклая и вогнутая гипотенуза), но если реально нарисовать два одинаковых треугольника с правильными гипотенузами и разрезать верхний на такие фигуры, то они не будут четко входить в нижний треугольник (друг на друга немного заходят). Вот и набегает клетка. А, и масштаб надо сделать как минимум раза в четыре больше. Попробуйте сами.
из-за раскладки фигур, получилась лишняя клетка. Это как в поход собирать рюкзак. Вы можете положить три вещи и больше ничего не влезет, а можете положить эти три вещи так, что еще пару вещей влезет.
Все дебилы, кто считает, что гипотенузы выпуклые и вогнутые!
нет там никаких выпуклых и вогнутых гипотенуз, все линии одноцветных фигур — прямые, но вот кто сказал, что большие фигуры — треугольники? ничего подобного! там два четырехугольника (дадада, эти фигуры так и называются, ибо понятия «не совсем треугольники» я что то в геометрии не встречал), причем разной площади. и площадь их отличается как раз на эту клетку. т.е. три вершины 4хугольника — это три явно видных вершины, а четвертая — общая точка красного и темно-зеленого треугольников. что бы увидеть, что угол там не 180 достаточно просто попробовать провести прямую линию через три точки гипотенуз красного и темно-зеленого треугольников, и увидеть, что это не получается.
в принципе, даже если присмотреться и к тому, что изображено и сравнить две фигуры не только по трем явным вершинам, но и по общим точкам красного и темно-зеленого треугольников — будет видно, что одноименные точки на двух фигурах не совпадают: на верхней фигуре, площадь которой меньше, обе точки ниже, чем на нижней.
Это не математическая задача
По словам Мартина Гарднера, эту задачу изобрёл иллюзионист-любитель из Нью-Йорка Пол Карри в 1953. Однако принцип, заложенный в неё, был известен ещё в 1860-е годы. Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи.
https://ru.wikipedia.org/wiki/Исчезновение_клетки
Ответ:
Секрет в том, что зеленый и красный треугольники имеют неравные углы, что визуально незаметно из-за слишком малой разницы. Поэтому на первом рисунке создаётся излом внутрь, а на втором — наружу. Это легко проверить наложением и вычислениями.
Площадь каждого треугольника 13×5 не равна площади частей, из которых они составлены. «Гипотенуза» на самом деле является ломаной линией.
Действительно, общая площадь четырёх частей равна 32 кв. ед., а площадь треугольника 13×5 равна 32,5 кв. ед. Отношение длин катетов синего треугольника 5:2, а красного — 8:3, поэтому эти треугольники не являются подобными, а значит, имеют разные углы. Гипотенузы в обоих треугольниках 13×5 на самом деле являются ломаными линиями. Если наложить треугольники 13×5 друг на друга, то между их гипотенузами образуется параллелограмм, в котором и содержится «лишняя» площадь.
я очередной раз повторяю, что вы несёте в массы ерунду! Про кривые гипотенузы, неподобные треугольники и прочие некоректные доказательства.
Сейчас я вам это в цифрах всё продемонстрирую…
Данная клетка будет появляться внезамисимости от того кривая гипотенуза или прямая. Воспользуемся всё той же ранееупомянутой мной «Арифметикой Пупкина с картинками».
Обозначим площади соответствующих треугольников как S1,S2,S3,S4. Теперь перевернём треугольник с полостью и положим его сверху до состояния «прямоугольник». Этот прямоугольник можно визуально разделить на два прямоугольника — левый Sл и правый Sп (как на нижней картинке). Теперь переходим непосредственно к арифметике : Площадь треугольников равна
S1=(2×5)/2 = 5
S2=(3×8)/2 = 12
S3= 8
S4= 7
Далее — Sп=S1+S1+S3+S4 = 25
А теперь самое интересное — площадь Sл=5х8 = 40 и будет состоять из S3+S4+S2+S2, а это равно не 40!!! Это равно 8+7+12+12=39!… Вот вам и лишний сороковый квадратик!… Я думаю, что при немного другом соотношении фигур этого пустого квадрата не будет. Насколько я помню — это как-то связано с последовательными числами Фибоначчи… Как то так…
распечатал вырезал лезвием совмещал. разницы не нашол. парадокс есть.
Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунках 2 и 3 — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Назовём первую фигуру, являющуюся вогнутым четырёхугольником, и вторую фигуру, являющуюся вогнутым восьмиугольником, псевдотреугольниками. Если нижние стороны этих псевдотреугольников параллельны, то гипотенузы в обоих псевдотреугольниках 13×5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем — наружу). Если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке 3 этот параллелограмм приведён в верных пропорциях.
Острый угол в этом параллелограмме равен arcctg 46[1] ≈ 0°1′18,2″. На такой угол минутная стрелка на исправных часах сдвигается за 12,45 с. Именно на такую величину тупой угол в рассматриваемом параллелограмме отличается от развёрнутого. Визуально столь ничтожное отличие незаметно.